[ゆるーい流体力学]粘土、動粘度?動き出すのに必要な力は?

流体の持つ性質で特に重要な性質に圧縮性と粘性がありますよね
このページではその中でもできるだけゆるーく粘度とその練習問題についてまとめていきます
このページでは水の流体力学について取り扱います
粘度
粘度とは粘性率のことです
言い換えればねばねばぐあいを表しています
水道水とあんかけのあんではあんのほうがどろっとしてますよね?笑笑
つまりこの2つではあんのほうが粘度が高いということになります

粘度の式
粘度については以下のようなケースを考えます
わかりやすいように流体は水だと想像してみてくださいね
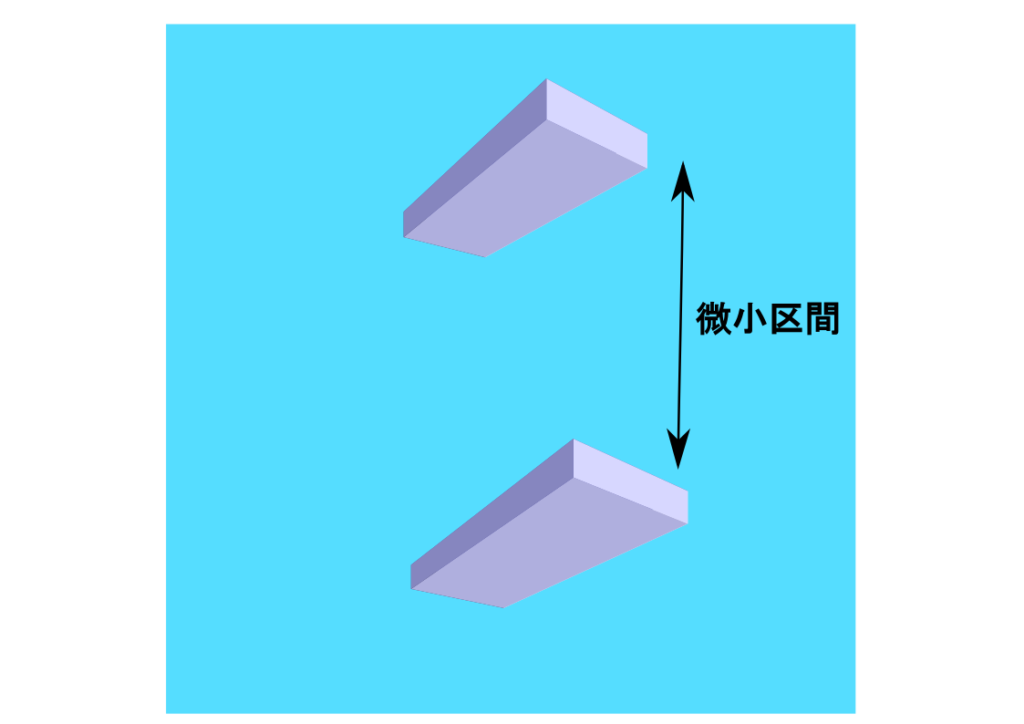
二つの板(向かい合う面の面積:$S\rm{[m^3]}$)を微小区間(距離:$h\rm{[m]}$)だけあけて、流体中(密度:$\rho\rm{[kg/m^3]}$)に配置しています
ここで、
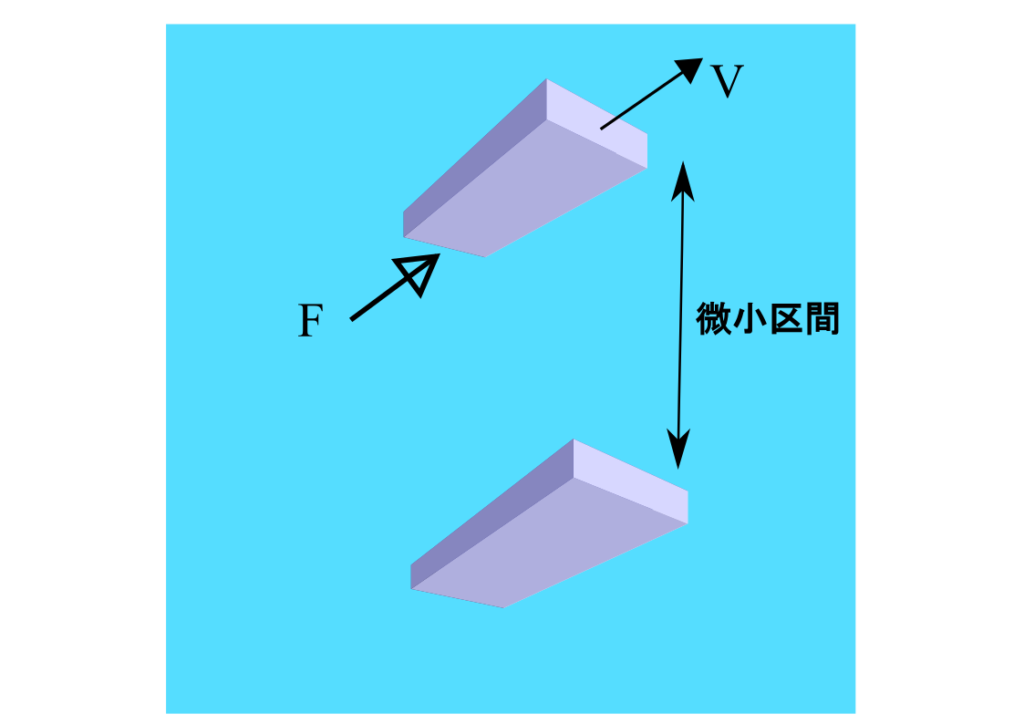
上側の板を力:$F\rm{[N]}$で押したときに、その板が速度:$V\rm{[m/s]}$で動き始めたとしましょう
この図の中で上の板を押すために必要な力は何に比例して何に反比例するのか
直感的に考えてみましょう
| 関係がありそうな値 | |
| $S$ | 板の面積(向かい合っている面積) |
| $V$ | 板が動き出した速さ |
| $h$ | 2つの板の距離 |
板を押す力は板の面積が大きいほど大きく、強く押せば動き出す速さも大きくなり、板の距離が開けば押す力は小さくなります
これは板の間を水でなくスライムなどで置き換えてみたほうが分かりやすいかもしれません
板の面積が大きくなると摩擦が大きくなるので板を押す力が必要になる、板の距離が離れるとその摩擦が小さくなるので力は少なく動かせる、、、そんな気がしませんか?
以上より以下の式が成り立ちます
$F\propto\frac{S\cdot V}{h}$
ここでこの比例式の比例定数を$mu$とおくと、
$F=\mu\cdot\frac{S\cdot V}{h}$
この\muを粘度(粘性率、粘性係数)といいます
水や空気をはじめ多くの流体はこの式に基づきます
そのようなものをニュートン流体といいます
(詳しくは板のずれによる剪断力:$\tau$に対して$\tau=\mu\cdot\frac{V}{h}$が成り立つものに対する)
動粘性係数
以上の粘性係数は物体が動き出すまでの値です
高校の力学でやった摩擦でいうところの静止摩擦係数ですね
ということはもちろん動摩擦係数と対応するものも存在します
それが動粘性係数(動粘度、動粘性率)です
先ほど粘性係数を考えた時の図をもう一度使います
使いますとは言いましたが考えることはあまりありません
今回も直感的に考えます
粘性係数を考えた時に用いたもの以外で動いているときに関係する値、それは流体の密度:$\rho\rm{[kg/m^3]}$です
ではこれは比例的に影響するか反比例的に影響するかですが、密度が増加すると動きにくくなることから考えると反比例的に作用することが分かります
渋滞すると車の密度が高まって動きにくくなりますよね?
以上より動粘性係数:$\nu\rm{[m^2/s]}$は、
$\nu=\frac{\mu}{\rho}$
で表されます!
完全流体、理想流体
今まで考えてきた粘性ですが、これを考えると計算がややこしくなってきます
そこで粘性のない仮想的な流体を考えることがあり、これを非粘性流体または完全流体と呼びます
またここでは詳しく触れませんが、前述の流体力学における重要な性質である圧縮性をさらに無視すると非圧縮性完全流体または理想流体といいます
液体の流体力学を扱う際、気体と異なってほとんど圧縮性がないため無視しても大丈夫です
練習問題
問1.
下図においてピストンを動かすために必要な力:$F\rm{[N]}$はいくらでしょうか?ただし、潤滑油の粘度:$\mu\rm{[kg/m^3]}$、ピストンの直径:$d\rm{[m]}$、ピストンの長さ:$l\rm{[m]}$、シリンダーの直径:$D\rm{[m]}$、ピストンが動き出す速度:$v\rm{[m/s]}$とし、ピストンとシリンダーは円柱状だとします
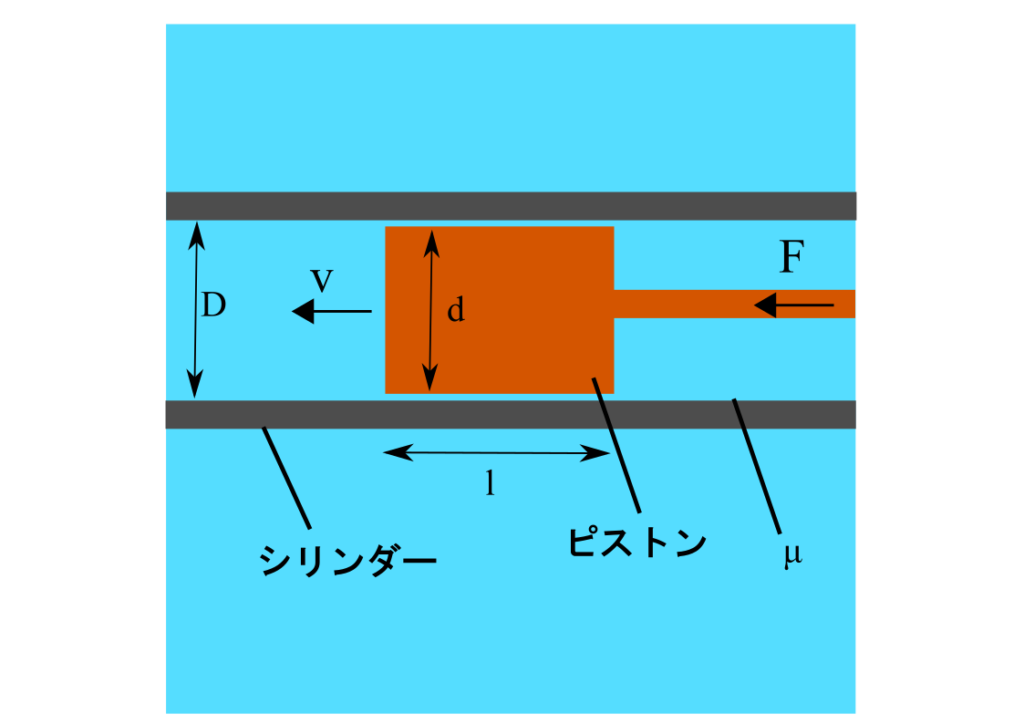
問2.
同条件下でピストンを押さずに回転させるとき、回すために必要なモーメント(トルク):$M\rm{[Nm]}$を求めましょう。この時に発生する回転角速度を$\omega\rm{[rad/sec]}$とします。
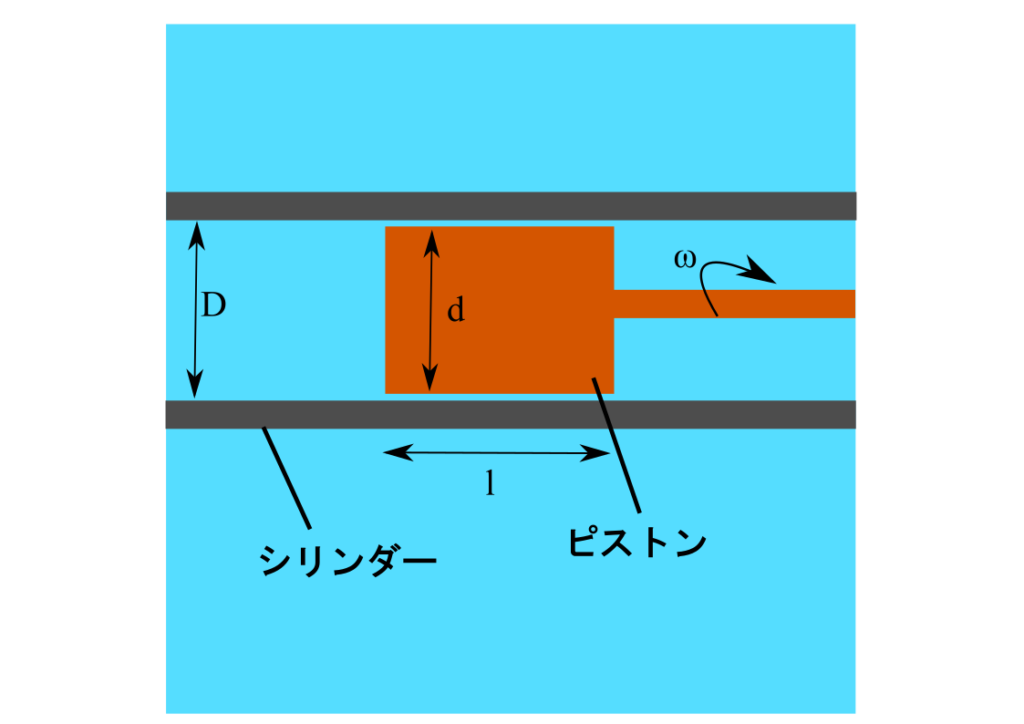
、、、どうでしょう?解けましたか?
それでは解説にうつります!
問1.
これは粘度の式にそのまま代入すれば解くことが可能です
\begin{align}
F &= \mu \frac{S\cdot V}{h} \\
&= \mu \frac {\pi dl \cdot v}{\frac{1}{2}(D-d)} \\
&= \frac{2\pi \mu dlv}{D-d} \rm{[N]}
\end{align}
問2.
円において微小角度回転した場所の円弧の長さは"半径"×"角度"であったことを思い出しましょう
そうしたら回転させるために必要な力は、
\begin{align}
F &= \mu \frac{S\cdot V}{h} \\
&= \mu \frac {\pi dl \cdot \frac{d}{2}\omega}{\frac{1}{2}(D-d)} \\
&= \frac{\pi \mu d^3l\omega}{2(D-d)} \rm{[N]}
\end{align}
よって回転させるためにはこの力がピストンの端を回転させるだけのトルクを持てばいいので、
\begin{align}
M &= F \cdot \frac{d}{2} \\
&= \frac{\pi \mu d^3 l \omega}{2(D-d)} \rm{[Nm]}
\end{align}
ディスカッション
コメント一覧
まだ、コメントがありません